Contributed by Mark Carson of Individual Design

If you’ve ever seen a watch with a slide rule bezel and haven’t known how to use it, we have a little guide for you. As many of you know, watches with slide rule functions have 2 logarithmic scales (the outer of which turns). In contrast, a tachymeter scale is hyperbolic and typically has numbers that run in from infinity down to sixty. Both slide rule and tachymeter watches use non-linear scales. Let’s look a bit at a generic scale.

NOTE – the images shown are a bit rough as they are not photographs of an actual circular slide rule. This scale might not look like all slide rule bezels, but there are analog indicators on most slide rule bezels so that the same functions can be used.

The following examples show some common uses of a circular slide rule:

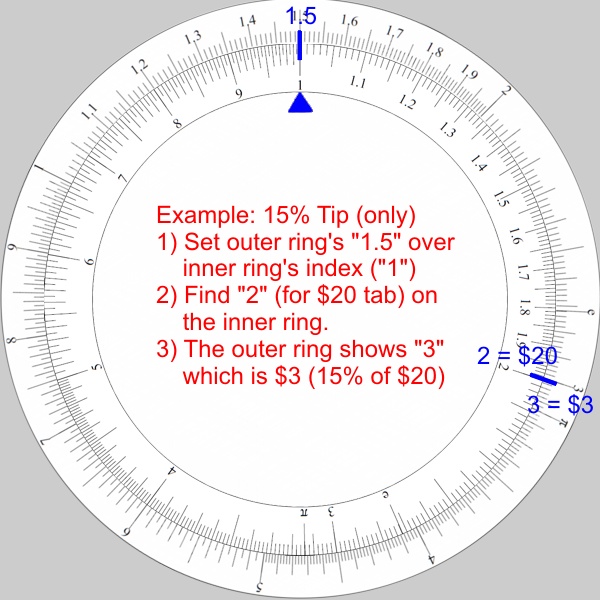
Calculating a 15% tip (I know, I’m cheap) – just the tip amount in this case:

• The goal: Calculate 15% of $20.00.
• Set the outer ring’s “1.5” (for 15%) over the inner ring index (“1”).
• Find “2” (for $20.00) on the inner ring.
• The outer ring shows “3” which is $3.00.
• So a 15% tip for a $20 tab is $3.00

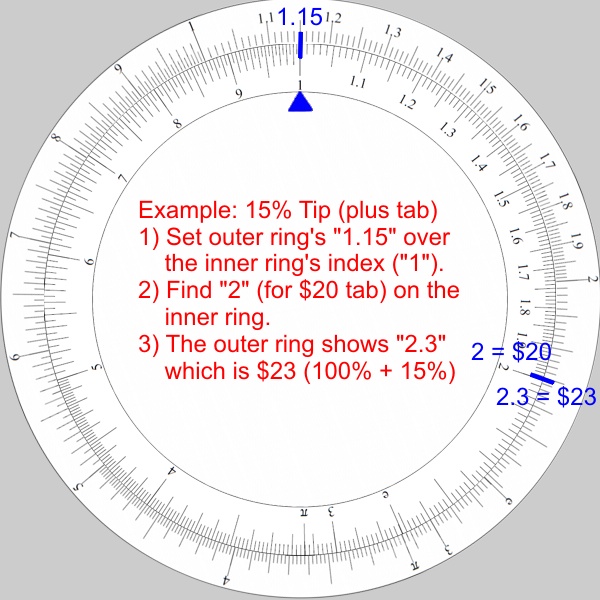
Calculating the total bill with a 15% tip (I’m still cheap):

• The goal: Calculate the total bill with a 15% tip on top of $20.00.
• Set the outer ring’s “1.15” (115% = 15% plus the base of 100%) over the inner ring index (“1”).
• Find “2” (for $20.00) on the inner ring.
• The outer ring shows “2.3” which is $23.00.
• So a 15% tip plus the $20.00 tab is $23.00 all together.

• 

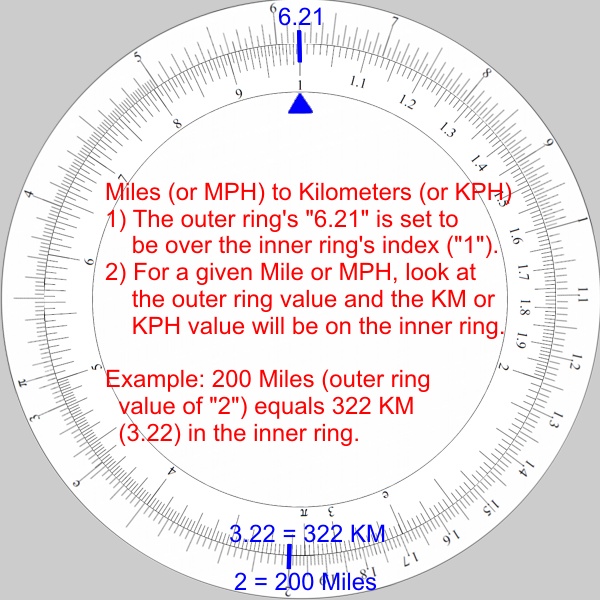
Miles or MPH to Kilometers or KPH conversions:

• The goal: Calculate a distance or speed in Kilometers where the distance or speed is known in Miles.
• A Kilometer is roughly 0.621 of a mile.
• Set the outer ring’s “6.21” over the inner ring index (“1”).
• Find “2” (for 200) on the outer ring.
• The inner ring shows “3.22” which is 322 kilometers.

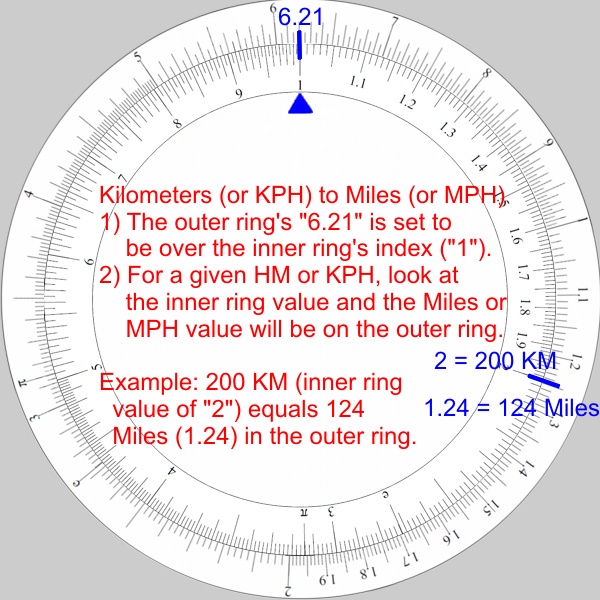
Kilometers or KPH to Miles or MPH conversions:

• The goal: Calculate a distance or speed in Miles where the distance or speed is known in Kilometers.
• A Kilometer is still roughly 0.621 of a mile.
• Set the outer ring’s “6.21” over the inner ring index (“1”).  No change from the previous example.
• In this case, we will technically be doing division rather than multiplication (dividing 200 by 0.621). Subtracting log values is division whereas adding log values is multiplication.
• Find “2” (for 200) on the inner ring.
• The outer ring shows “1.24” which is 124 miles.

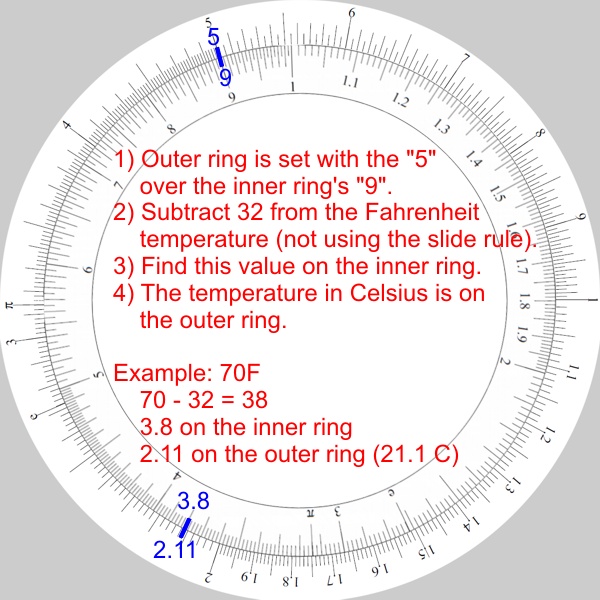
Fahrenheit to Celsius temperature conversion:

• The goal: Calculate the Celsius temperature where the Fahrenheit value is known.
• Celsius has 100 degrees between boiling (100) and freezing (0) while Fahrenheit has 180 degrees between boiling (212) and freezing (32). So 100/180 = 5/9. This is the fractional value (ratio) of a Fahrenheit to a Celsius degree. Each degree “F” is 5/9 of a degree “C”. The actual temperature “F” also needs 32 added to it as freezing is 32 F.
• This one is a bit advanced as it starts with 5 over 9 on the slide rule instead of the usual staring with the index (“1”) beneath a factor.
• Set the outer ring’s “5” to be over the inner ring’s “9”.
• Subtract 32 from the Fahrenheit temperature (not using the slide rule).
• Find this subtraction value on the inner ring.
• The outer ring show the temperature in Celsius.
• For example:
  • Convert 70 F to Celsius:
  • 70 – 32 = 38 (not using the slide rule).
  • Set the outer ring’s “5” to be over the inner ring’s “9”.
  • Find 3.8 (for 38) on the inner ring.
  • The outer ring shows 2.11 which means 21.1 degrees C.

I hope these help you to use slide rule watches more effectively (like the Breitling Navitimer recently reviewed here).

Author Mark Carson’s note: I grew up in the ancient days before electronic calculators. My father, being an engineer, used slide rules and taught me how to use one when I was about 12. I preferred circular slide rules. While their inner scales lack precision, an advantage of a circular slide run is that you never have to move the center slide back to the other end when you exceed the scale on one end.  And that makes them good for  visualizing that a logarithmic scale conceptually have no beginning or end,  it just keeps rolling around from 1.0 to, well, 1.0 at the next order of magnitude. Sometimes people ask, how will I know if the answer is 1.1 or 11 or 111, etc. As my father used to drill into me, you have to “know” the answer  already (roughly) in your head. A slide rule only gives you precision. That is, you know for a $20 restaurant tab plus a 15% tip, the total won’t be either 23 cents or $230. So, it must be logically be $23.

[phpbay keywords=”slide rule bezel” num=”6″ siteid=”1″ category=”14324″ sortorder=”EndTimeSoonest” templatename=”columns” columns=”2″ paging=”true”]